Multi-material mixing

In the study of multi-material mixing, we are currently implementing and validating multifluid algorithms. Based on the problems of interest (turbulent mixing in multi-material flows, e.g., compressible Rayleigh-Taylor instability, Richtmyer-Meshkov instability), flows of multiple non-reacting fluid components are considered. A certain class of schemes is selected; specific properties of the schemes are identified as essential to carry out direct numerical simulations and a suite of benchmark is defined to test these properties.

In accelerated multi-material flows (e.g., Rayleigh-Taylor and Richtmyer-Meshkov instabilities), the turbulence evolution is different from the classical shear-dominated turbulence of aeronautical applications. Interactions between shock waves and density variations (e.g., interface) lead to baroclinic vorticity generation along the interfaces. Instabilities are active on multiple scales: at the macroscopic level, they lead to the deformation of certain flow structures, while they drive the turbulent mixing at the microscopic level. Regions of high vorticity then evolve into turbulent mixing zones. Material interfaces are thin regions over which the composition changes from one fluid to another. Because the focus of the present work is on mixing, an interface-capturing approach is pursued, as opposed to interface-tracking and in analogy to shock-capturing. Because the interface is smeared over a few grid points, it is important that the dissipation of the scheme is low. Additional properties essential for stable and accurate simulations include discrete conservation and the prevention of oscillations at discontinuities (interfaces and shocks) that may have large jumps in pressure and/or density across them.

Quasi-conservative schemes extended to high-order accuracy are considered here in the context of the Hybrid method. In these scheme, supplementary advection equations (for the mass fraction and/or for a function of the ratio of specific heats) are solved in conjunction with the equations of motion. These schemes have currently been implemented in a multi-dimensional finite volume shock-capturing framework and can be used to simulate various multicomponent flow problems. An example thereof includes the two-dimensional shock-bubble interaction shown in figure 1. In this problem, the baroclinic vorticity generated by the passage of the shock leads to the formation of a re-entrant jet; complex flow features can be observed and regions of low pressure (high vorticity) are present.

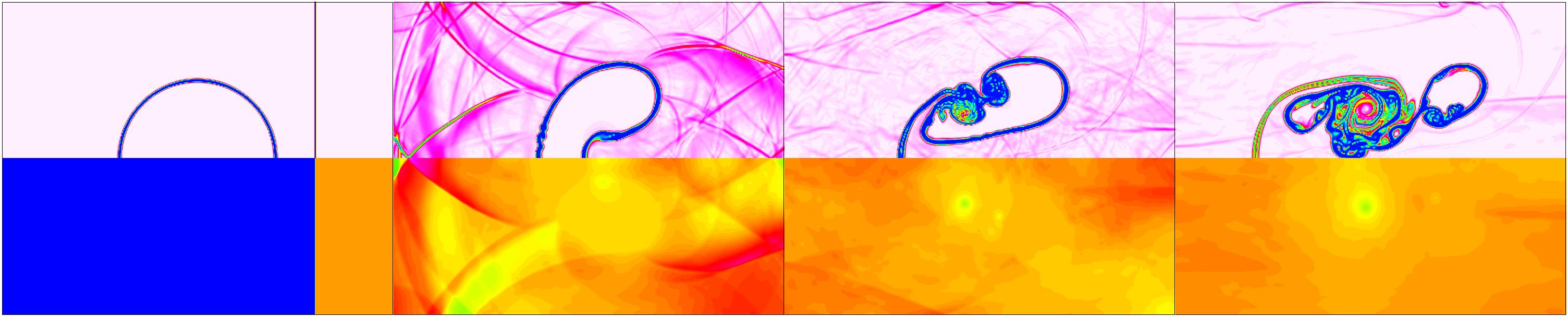
Figure 1. Interaction of a left-moving Mach 1.22 shock wave in air with a helium cylinder (top: numerical Schlieren; bottom: pressure).

The quasi-conservative schemes are currently being implemented in a finite difference framework into the Hybrid code. The treatment of interface is similar to that of shockwaves, in that an interface sensor (e.g., based on the mass fraction field) is required. Thus a high-order accurate WENO scheme is used near interfaces, similarly to shock waves, in order to prevent the generation of spurious oscillations. Each of the codes considered in the present SciDAC project will undergo a series of stringent test problems to evaluate its performance in multifluid problems. The careful development of the multifluid algorithm and its verification via the stringent suite of test problems is crucial in order to successfully simulate the multi-material problems of interest, i.e., compressible Rayleigh-Taylor instability and Richtmyer-Meshkov instability, and to study certain specific aspects, e.g., turbulent mixing and sub-grid modeling.