Numerical methods

One distinguishing component of the present SciDAC project is the assessment and development of numerical methods suitable for problems with interactions between turbulence, shock waves, and material interfaces. Computational turbulence is a field where the subtle details of the numerical method can have a dramatic impact on the accuracy of the results -- one may even draw the wrong scientific conclusions if one is not careful. The literature is filled with numerical methods that perform well on shock waves or turbulence in isolation, but much less is known about how these methods treat shocks and turbulence simultaneously.

The computational challenge of predicting shock/turbulence interactions stems from the fundamentally different physics at play. Shock waves are thin regions wherein flow properties change rapidly over a distance roughly equal to the molecular mean free path; hence, they are essentially strong discontinuities in the flow field. Turbulence, on the other hand, is a chaotic phenomenon with broadband spatial and temporal scales of motion. Most shock-capturing methods rely on strong numerical dissipation to artificially smooth the discontinuity, such that it can be resolved on the computational grid. However, the artificial dissipation necessary for capturing shocks has a deleterious effect on turbulence. An additional problem is the fact that shock-capturing schemes are typically based on one-dimensional Riemann solutions that are not strictly valid in multiple dimensions. This can lead to anisotropy errors and grid-seeded perturbations. Other complications arising from upwinding, flux limiting, operator splitting, etc..., can seriously degrade performance and generate significant errors.

The first milestone of the present project is a comparison between a set of promising methods on a carefully chosen suite of benchmark problems. We have divided this item into two sub-items, by first considering single-fluid cases only. The chosen single-fluid problems represent the key physics with increasing complexity:

1. Taylor-Green vortex: tests the accuracy and numerical stability on broadband turbulence without shocks.
2. Spherical Noh implosion: tests the capability to achieve full shock compression, correctly predict the shock speed, and maintain spherical symmetry on an infinite Mach number shock without turbulence.
3. 1D Shu-Osher problem: tests the capability of predicting a shock/entropy interaction, specifically to avoid damping of the post-shock entropy fluctuations.
4. 2D shock/entropy/vorticity interaction: extends the 1D Shu-Osher problem to two dimensions, with the associated induced unsteady shock-movement.
5. High-Mach number decaying turbulence problem: includes broadband vortical, acoustic, and entropy motions, as well as turbulence-induced weak shocks.

We point out that this benchmark study was undertaken in the spirit of learning about the strengths and weaknesses of different numerical approaches, with the obvious hope of devising future improvements. Therefore all problems were computed by four different numerical methods (i.e., codes) without ad hoc "tuning" for each problem. It is important to realize that most methods can be "tuned" to give accurate results for the first four benchmark problems -- but in the process sacrificing accuracy (or even stability) on the remaining problems. No such tuning was performed here. The four codes all represent different computational approaches, but every one could be considered state-of-the-art within its context. A brief summary of each code is given here:

1. The Miranda code (Cook, Phys. Fluids 2007}) uses very high-order operators (8th-10th order) to approximate the Navier-Stokes equations, with augmented artificial fluid properties (like viscosity) to capture shocks and other discontinuities. The guiding philosophy behind this method is to first regularize the equations (through the artificial properties) and then to solve the regularized equations using a very high-order method. The code has been run on up to 65,536 processors on the BlueGene/L machine.
2. The Hybrid code (Larsson et al., CTR Annual Research Briefs 2007) is based on the guiding idea that turbulence and shock waves are fundamentally different phenomena and thus should be treated by different numerical methods. Hence the Hybrid method relies on a sensor to identify regions of shock waves, and then applies a shock-capturing (WENO) scheme in these regions with a high-order central difference scheme elsewhere. This hybridization ensures minimal numerical dissipation in the method. The code has been run on up to 4,096 processors on the Franklin Cray XT-4 machine.
3. The ADPDIS3D code (Yee and Sjogreen, J. Comput. Phys. 2007) combines the best of non-dissipative high order spatial schemes with shock-capturing methods via an efficient containment of numerical dissipation. These low dissipative high order methods include limiting and filtering with flow sensors. Flow sensors are used as an adaptive procedure to analyze the computed flow data and indicate the amount, location and type (e.g., spectral filter, compact filter or nonlinear (shock) filter) of built-in numerical dissipation that can be eliminated or further reduced. Such a filter method consists of two steps, a full time step using a spatially high order non-dissipative base scheme, followed by an adaptive multistep filter consisting of the products of wavelet-based flow sensors and linear and nonlinear numerical dissipations. The idea to control numerical dissipation is very general and can be used in conjunction with high order spectral, spectral element, finite volume and finite difference compact or non-compact central spatial base schemes. Any shock-capturing scheme can be used as nonlinear dissipation, (e.g., the dissipative portion of the TVD, MUSCL, or (W)ENO methods), usually with flux limiters. The linear filter can be the standard spectral or compact filter, or the product of a high-order linear dissipation and an appropriate flow sensor. By design, the flow sensors, spatial base schemes, and linear and nonlinear dissipation models are stand-alone modules. Therefore, a whole class of low dissipative high-order filter schemes can be easily derived. With this family of adaptive filter schemes, a wide spectrum of flow regimes can be simulated using the same code. Central spatial base schemes of order up to 14 and the dissipative portion of shock-capturing schemes of order up to 9 have been implemented.
4. The final code differs from the others by using shock-fitting, rather than shock-capturing, to handle the shock waves. In other words, the exact shock-jump relations are imposed at the shock, which is therefore treated exactly. The method yields superior accuracy for geometrically simple shocks, but has yet to be applied to truly complex shock-structures.

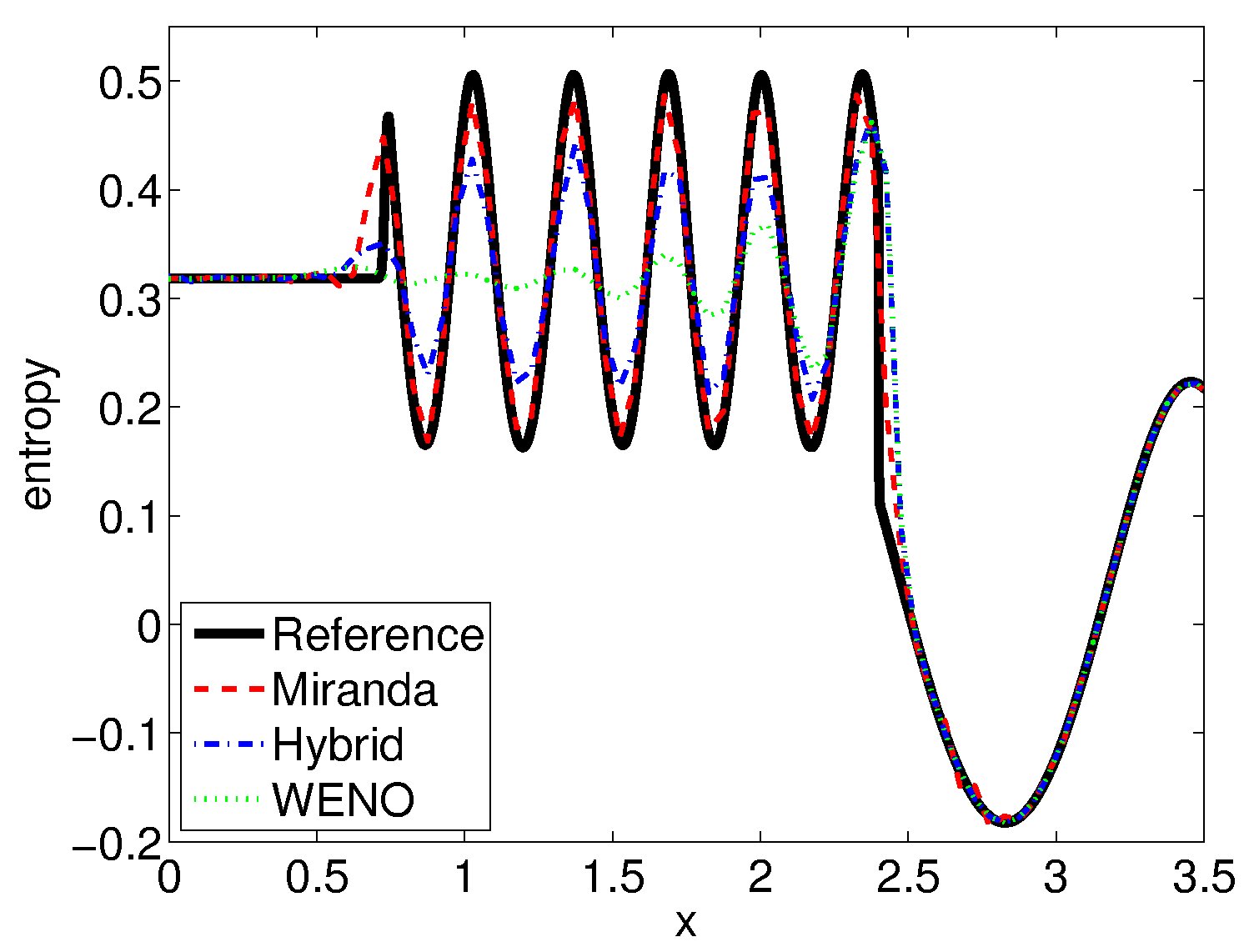
Figure 1. Entropy profiles after shock-turbulence interaction. Results show that: 1) the Miranda code performs extremely well on density disturbances; 2) standard WENO is highly dissipative, which kills the entropy fluctuation; 3) the Hybrid approach significantly improves on this, despite using the identical WENO scheme a the shock.

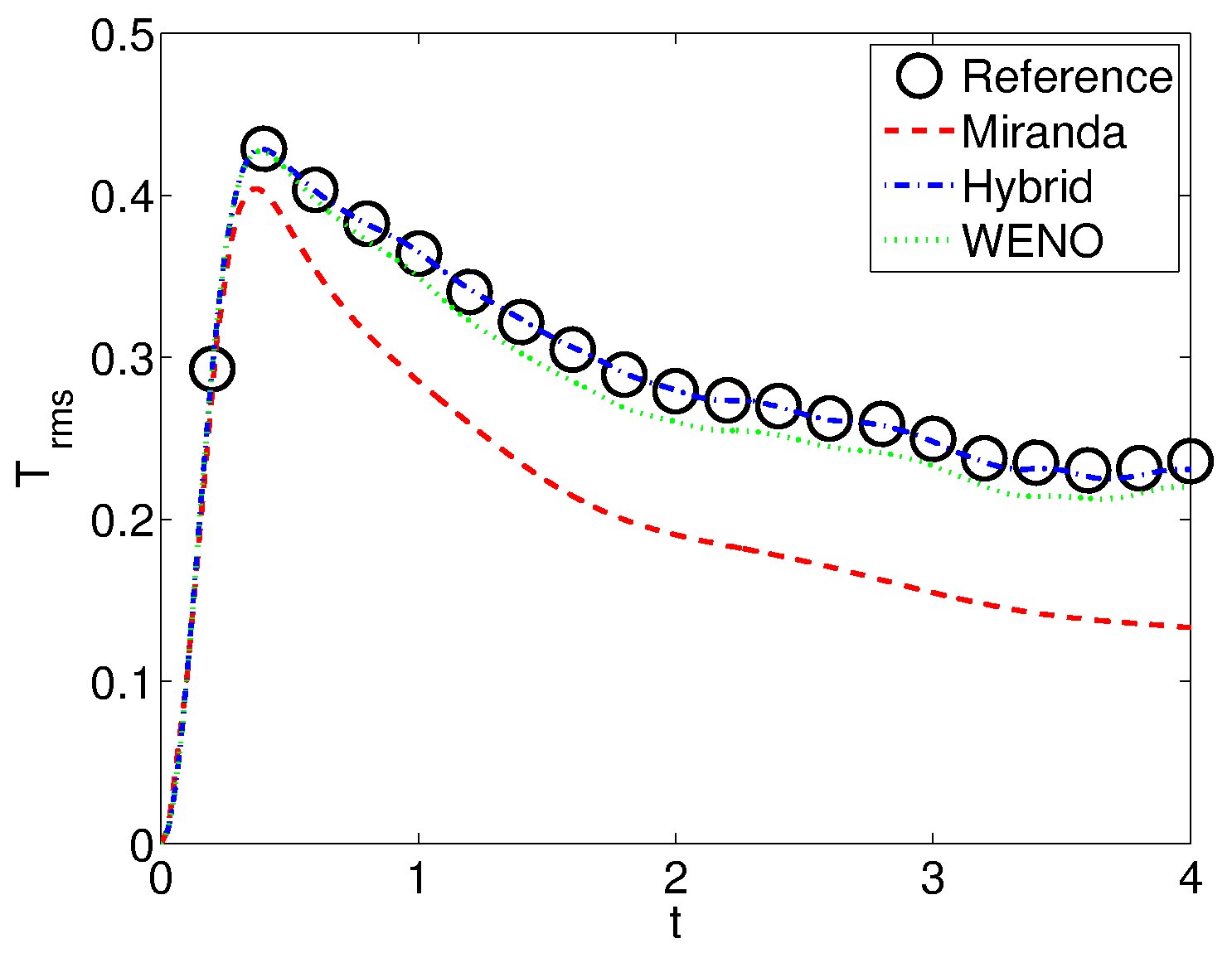
Figure 2. Temperature rms-profiles in decaying isotropic turbulence. Results show that: 1) The Miranda code excessively damps thermodynamic fluctuations; 2) standard WENO and the Hybrid method are less dissipative.

The benchmark comparison has brought several points to the surface. Most important is that the comprehensive nature of the problem suite has unmercifully brought out some of the weaknesses in every method, and one could argue that some of these findings were made possible only through the comprehensive suite.  Figure 1 shows the profiles of entropy after the shock-interaction in the Shu-Osher problem. The standard WENO method is severely dissipative, and the Hybrid philosophy of minimizing the dissipation by switching schemes is a vast improvement. The Miranda method is highly accurate for this problem, being capable of essentially capturing the full entropy fluctuation even on this coarse (200 points) grid. Figure 2 shows the evolution of temperature fluctuations in decaying isotropic turbulence on coarse (64^3) grids. Here the results are the opposite: this shows how the behavior of numerical methods on computational turbulence with shock waves is complex. The under-prediction by the Miranda method is most likely caused by the artificial bulk viscosity; improvements to the method that alleviate this issue have been and continue to be investigated.

In addition to the sample giving above, some other findings from the comprehensive assessment include:
1. While high-order WENO schemes are state-of-the-art in terms of handling pure shock waves, they add significant numerical dissipation on broadband turbulence and decrease the well-resolved range of scales by a factor of two or more.
2. The solution-adaptive philosophy in the Hybrid method drastically reduces the numerical dissipation, leading to much more accurate treatment of broadband turbulence.
3. More work is needed on reliable shock sensors, that work in a broad range of problems.
4. The Miranda treatment of shocks through artificial fluid properties works well on well-resolved motions, but needs improvement on broadband turbulence.